1
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history This answer is not useful Show activity on this post In Mathematica tongue x^2 y^2 = 1 is pronounced as x^2 y^2 == 1 x^2y^2=1 It is a hyperbola, WolframAlpha is verry helpfull for first findings, The Documentation Center (hit F1) is helpfull as well, see Function Visualization, Plot3D x^2 y^2 == 1, {x, 5, 5}, {y, 5, 5}
Derivative of 1/sqrt(x^2+y^2+z^2)
Derivative of 1/sqrt(x^2+y^2+z^2)-Graph x^2y^2=1 x2 y2 = 1 x 2 y 2 = 1 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from theOnce you set $z=x^2y^2$, then things get extremely simple Indeed $$ z'=2x2yy'=2\sqrt{x^2y^2}=2z^{1/2}, $$ and hence (assuming that $z>0$) $$ z^{1/2}z'=2, $$ or $$ \big(z^{1/2}\big)'=1, $$ or $$ z^{1/2}=xc $$ for some constant $c$, and finally $$ z=(xc)^2, $$ equivalently $$ x^2y^2=(xc)^2, $$ and hence $$ y^2=2cxc^2 $$
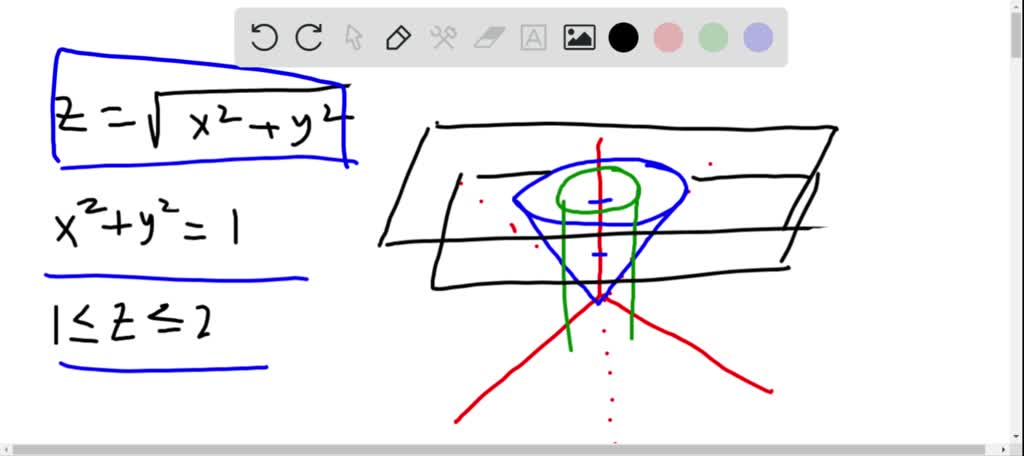
Solved Sketch The Region Bounded By The Surfaces Z Sqrt X 2 Y 2 And X 2 Y 2 1 For 1 Leqslant Z Leqslant 2
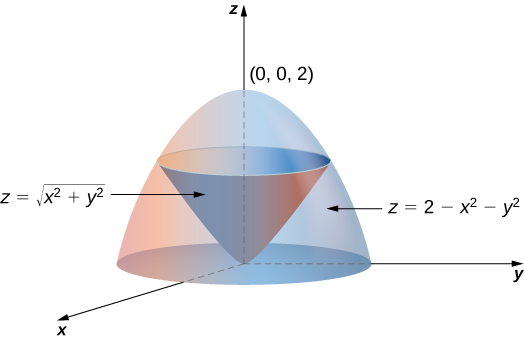
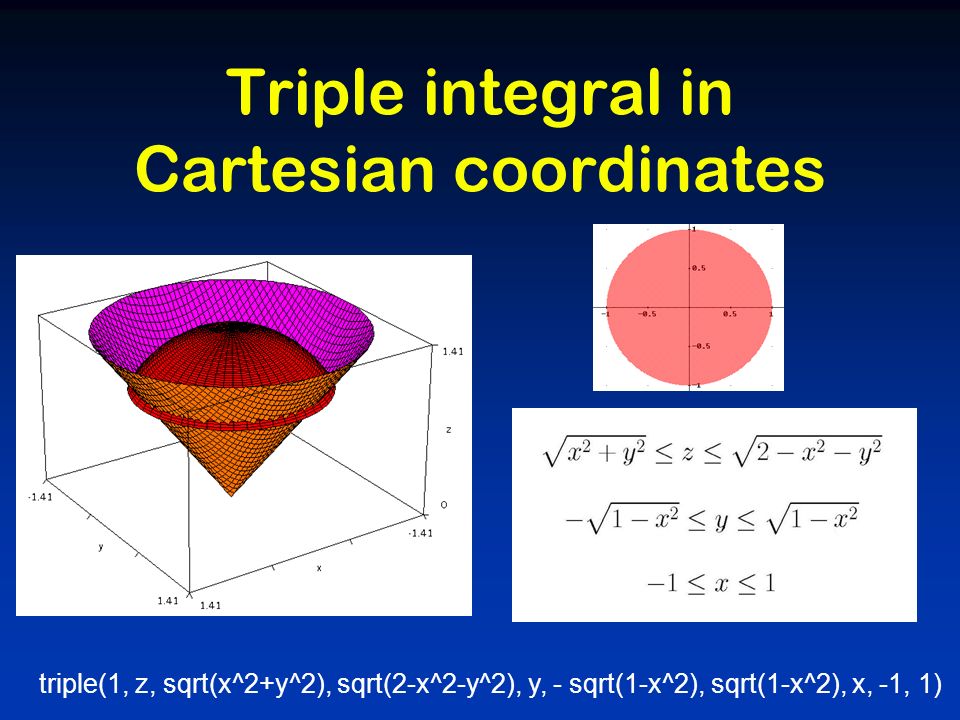
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange Example 1553 Setting up a Triple Integral in Two Ways Let E be the region bounded below by the cone z = √x2 y2 and above by the paraboloid z = 2 − x2 − y2 (Figure 1554) Set up a triple integral in cylindrical coordinates to find the volume of the region, using the following orders of integration a dzdrdθExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music
1/ (sqrt (2)) \square!Vector field plot (x/sqrt(x^2y^2), y/sqrt(x^2y^2)) Natural Language; ```(dz)/(dx) = 1/sqrt(x^2 y^2) (d/(dx) sqrt(x^2 y^2))` since `d/(dx) ln(f(x)) = (f'(x))/f(x)` `d/(dx) sqrt(x^2 y^2) = (1/2)(x^2y^2)^(1/2)(2x) = x/sqrt(x^2y^2)`
Derivative of 1/sqrt(x^2+y^2+z^2)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
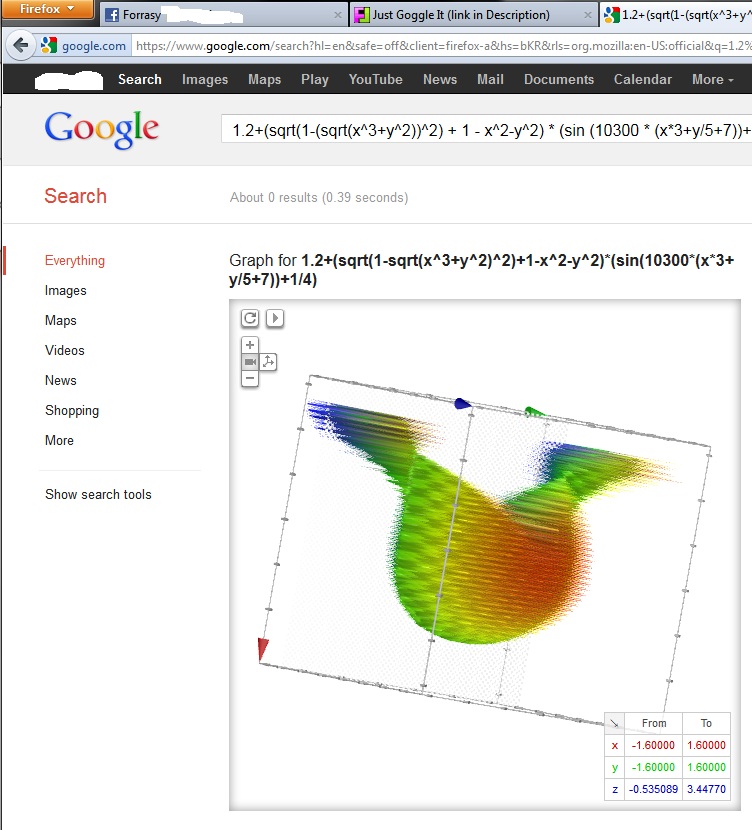
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 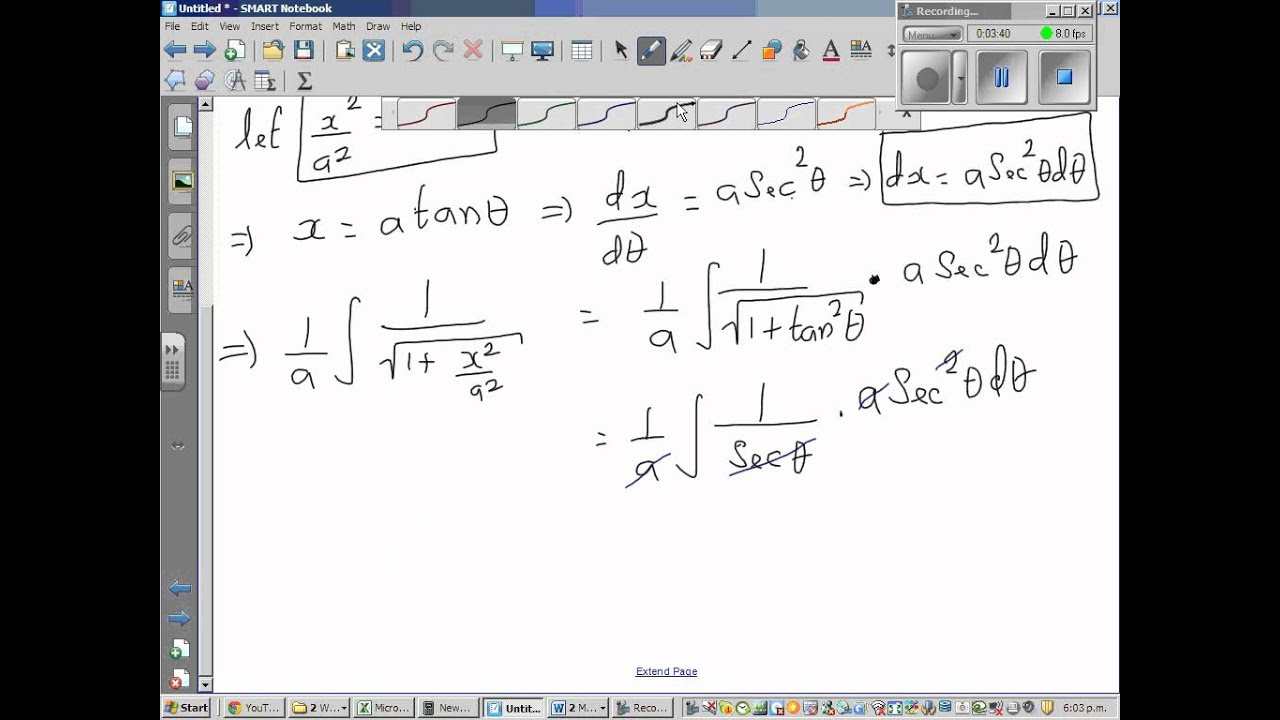 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 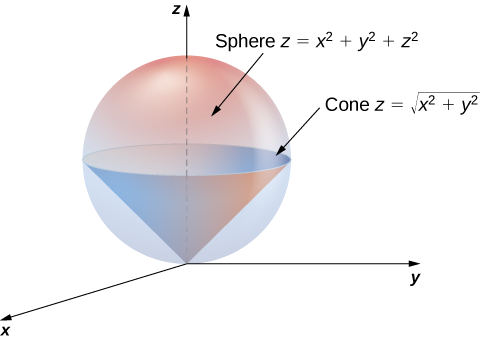 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 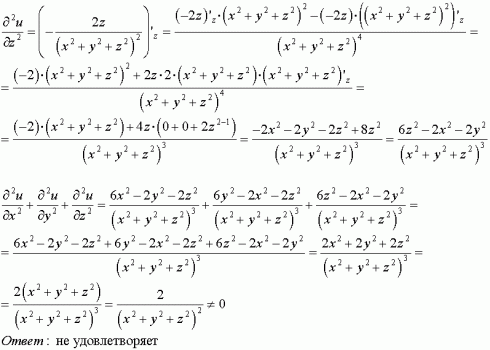 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 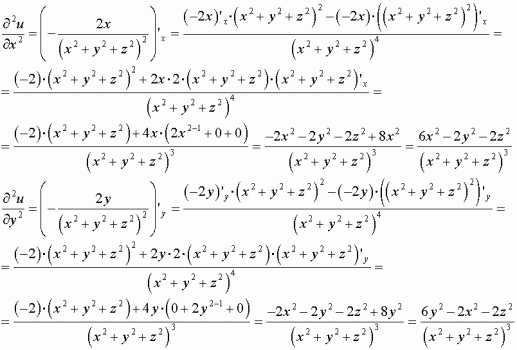 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 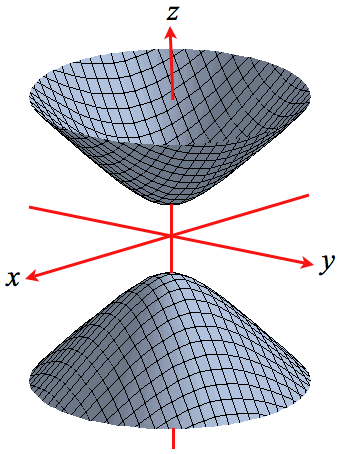 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 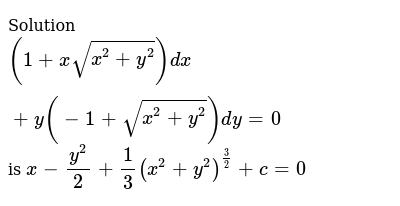 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
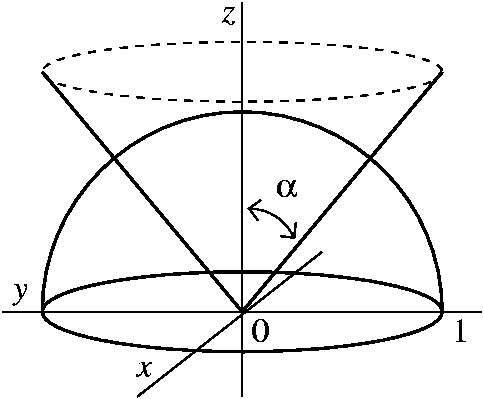 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 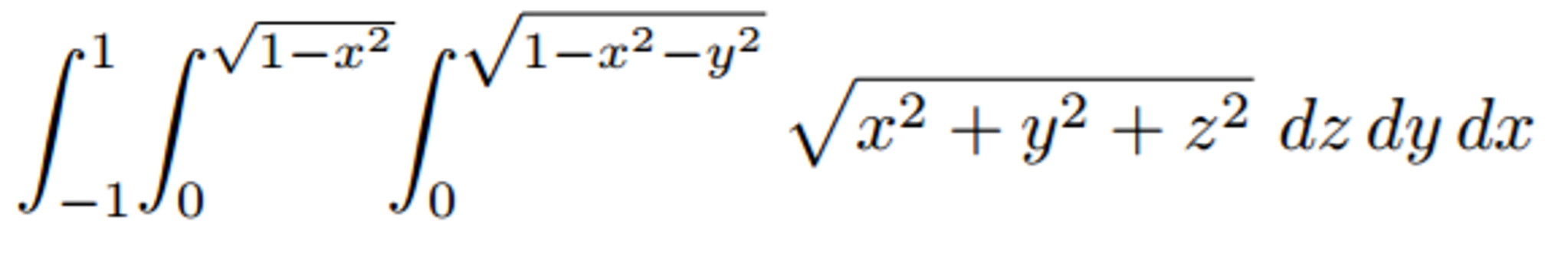 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 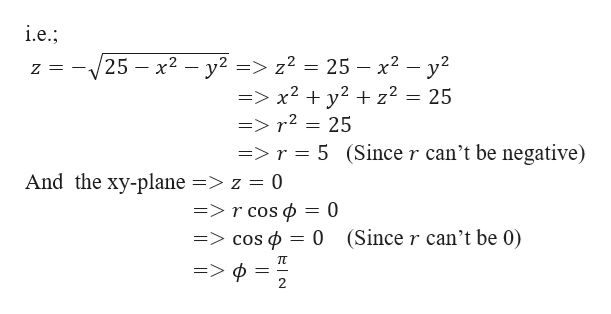 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 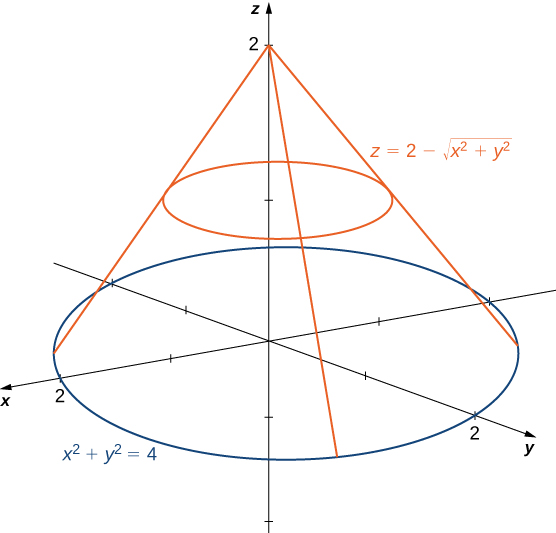 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 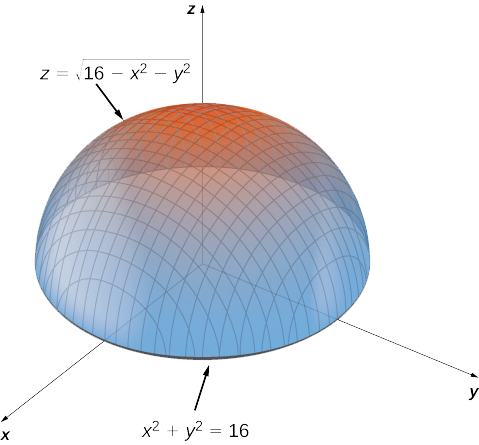 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 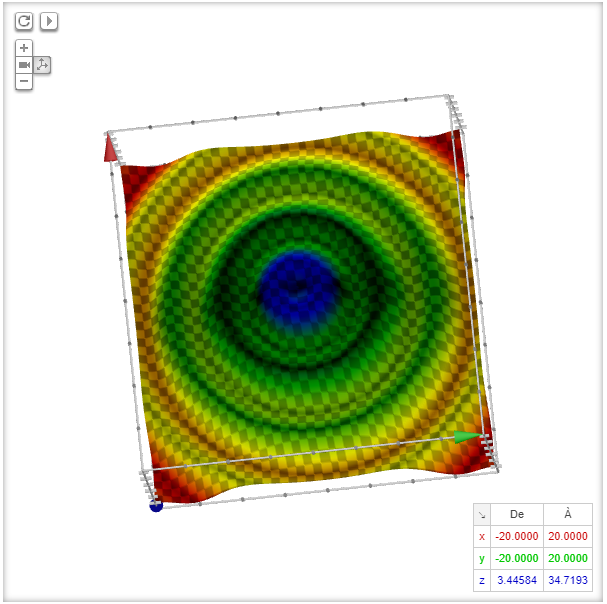 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 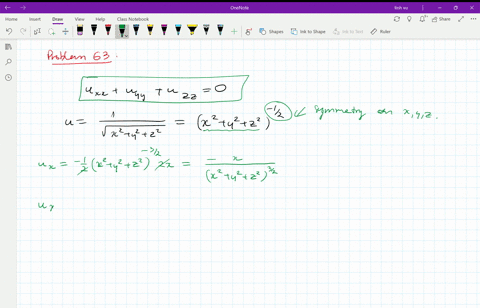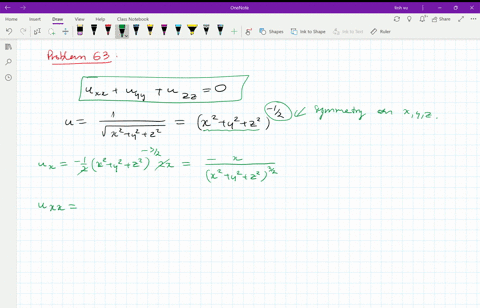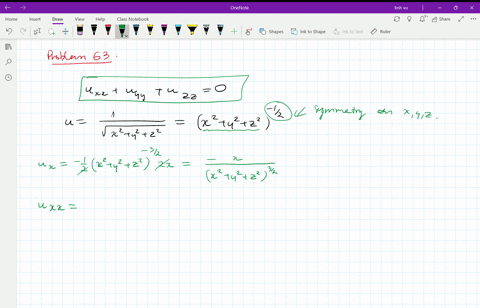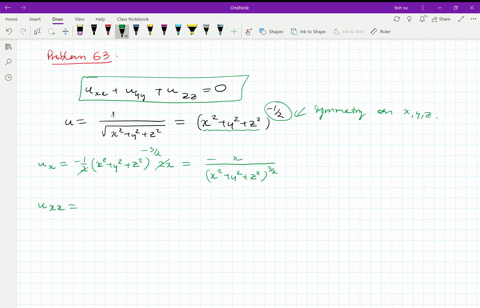 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 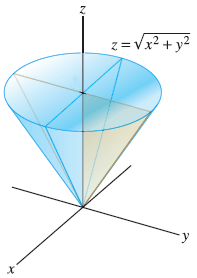 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 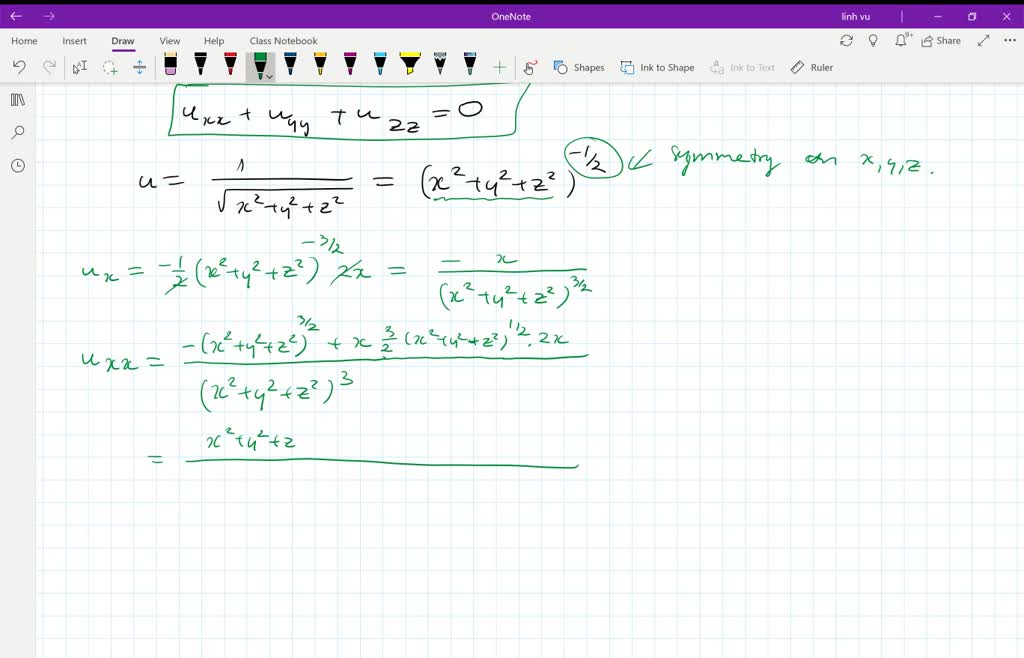 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 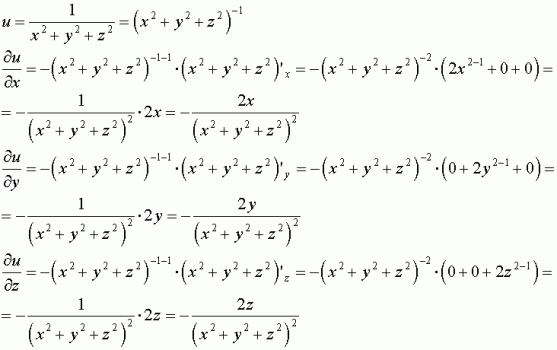 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 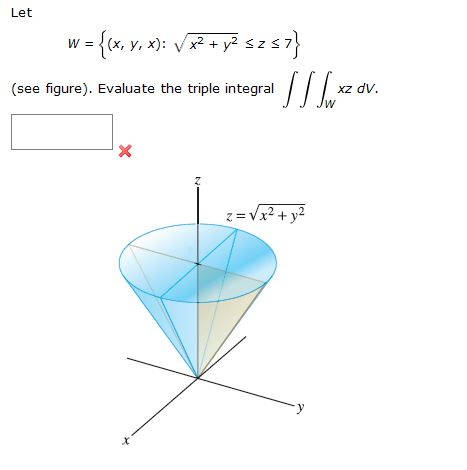 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
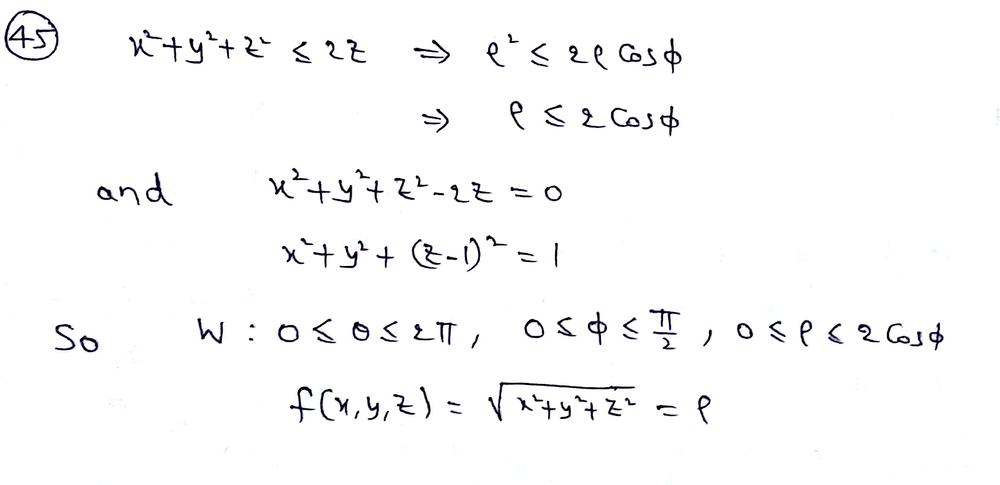 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 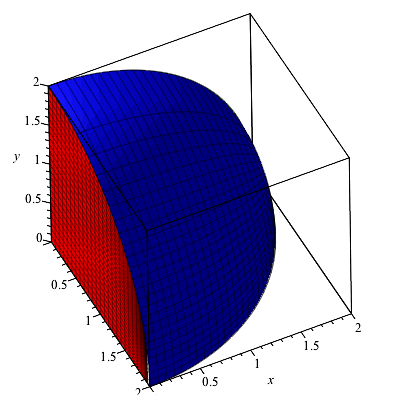 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 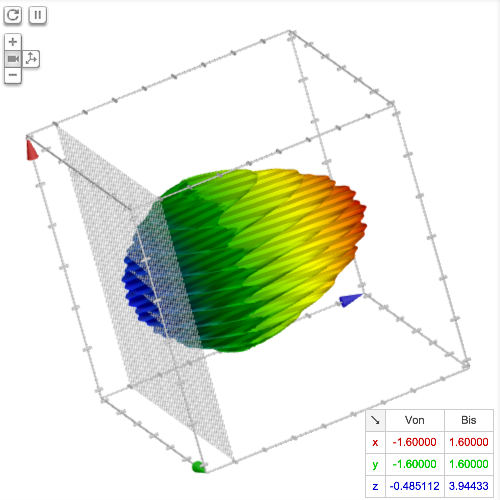 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
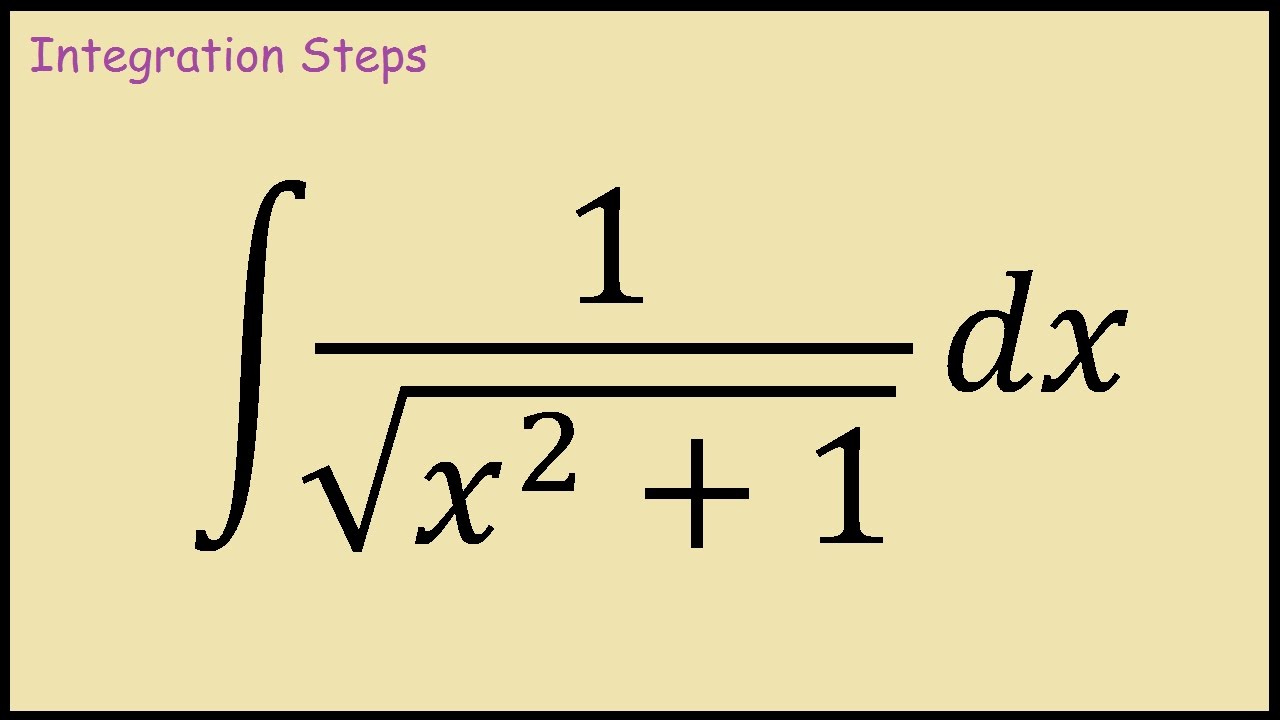 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 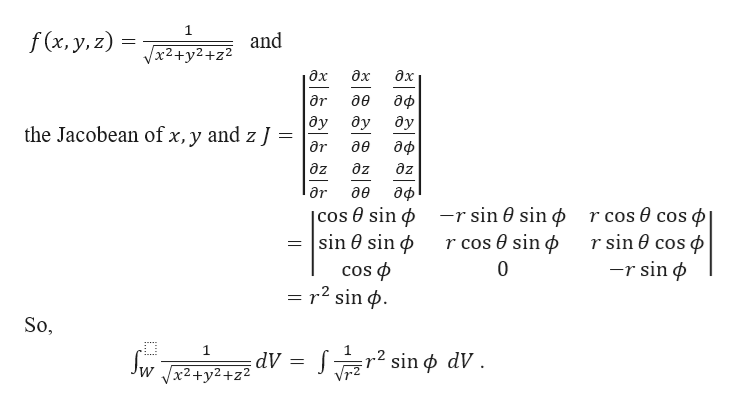 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux | 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |  1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 Recherche Google No Flux |
Answer (1 of 3) I assume you want to integrate this \displaystyle{\iint\dfrac{x}{\sqrt{x^2y^2}}dxdy} We should probably switch to polar coordinates, because {\sqrt{x^2y^2}}is an expression that perfectly relates polar and Cartesian coordinate systems Let x=r\cos(\theta)and y=r\sin(\theta)Limit as (x,y) approaching (0,0) of (x^2y^2)/(sqrt(x^2y^21)1) Derivatives First Derivative;
Incoming Term: 1/sqrt(x^2+y^2+z^2), u=1/sqrt(x^2+y^2+z^2), integral 1/sqrt(x^2+y^2+z^2), laplacian of 1/sqrt(x^2+y^2+z^2), derivative of 1/sqrt(x^2+y^2+z^2), partial derivative of 1/sqrt(x^2+y^2+z^2), triple integral of 1/sqrt(x^2+y^2+z^2), evaluate the triple integral 1/sqrt(x^2+y^2+z^2), verify that the function y=1/sqrt(x^2+y^2+z^2),




0 件のコメント:
コメントを投稿